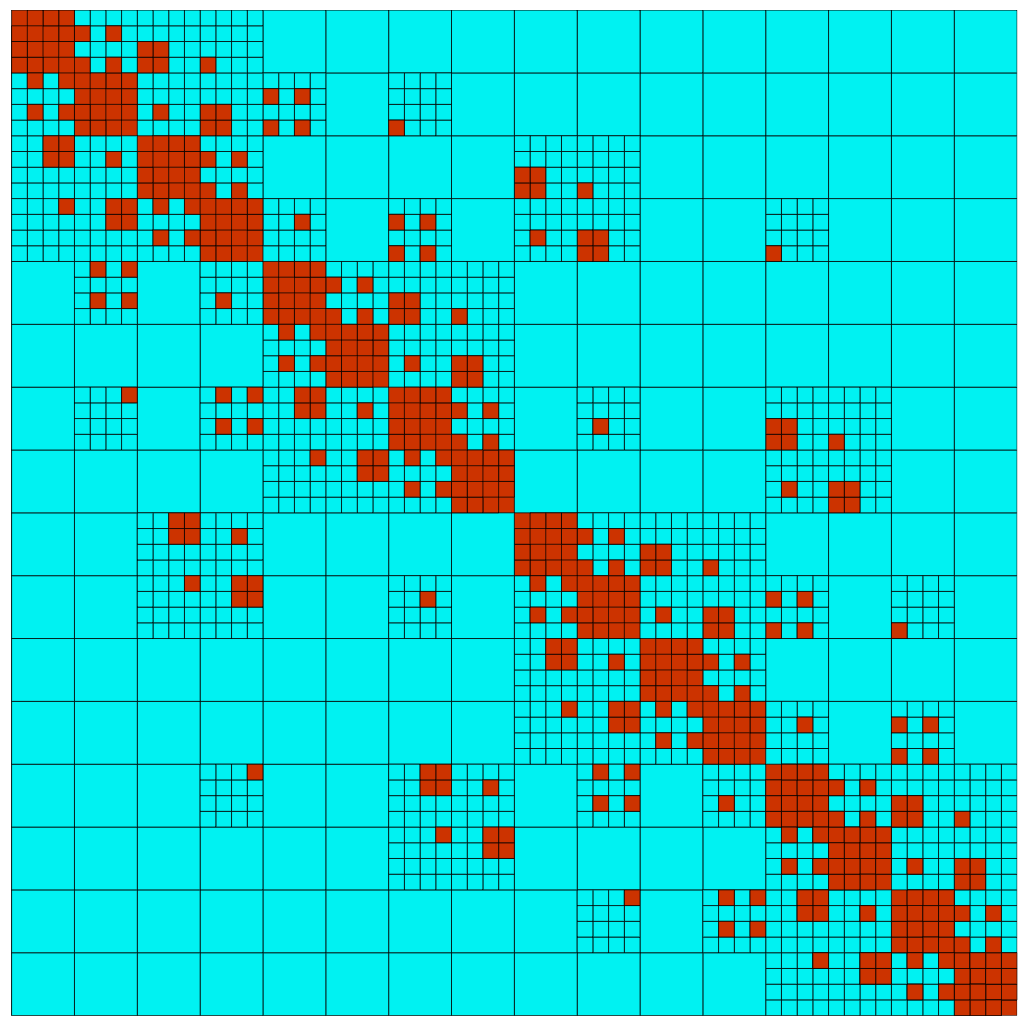
Runtime improvement of Poisson equation solver using Hierarchical Matrix concept
Dual Degree Project (M.Tech thesis) during my 5th year at Indian Institute of Technology (IIT) Madras. I was working under the supervision of Head of Department of Mathematics, Prof. S. Sundar. This project was an extension of a course project in Prof. Sundars course on Computer Modeling & Simulation during my 4th year.
Languages:
- C++
Libraries:
- Eigen (linear algebra)
- HLibPro
This project was an extension of a course project from Computer Modeling and Simulation, taught by Prof. Sundar. I programmed a lid driven solver based on Finite Pointset Method (FPM) in Python. At one of the substeps in the time iteration loop, solution to a Poisson’s equation is required. The aim of this project was to speed up the solution to this equation by using a suitable pre-conditioner. The problem a finding a suitable pre-conditioner is time consuming, and sometimes takes even more time than finding the direct solution. The idea here was to use Hierarchical Matrix concept, introduced in 1999, to compress the LHS matrix to a H-matrix format and utilize the efficient algebra operations defined on these class of matrices to find a suitable pre-conditioner in a reasonable amount of time.
Although a commerical library for research purposes was available on internet, I programmed my own library in C++ as it helped reinforce the concepts and provided a benchmark. For building a H-matrix from a given matrix, we first constructed an index tree for the row and column indices of the matrix. This was achieved using graph clustering algorithm: Heavy Edge Matching. After the clustering tree, we used the graph obtained in each step to reconstruct each level of the index tree. As the clustering can result in pairs of non-adjacent indices on any level, we used a permutation matrix to reorder the original matrix to ensure the indices were clustered in a chronological order. Next, we performed a cartesian product of the index trees. This resulted in a block cluster tree and each node in this (quad) tree represents a sub-matrix inside the original matrix. Some of such nodes can be compressed using algorithms such as SVD, r-SVD, which are marked using an admissibility condition. The block cluster tree was finally used to construct the H-matrix.
A comparison of my library and the commercially available packge showed us that my library was slightly slower than HLibPro. So, for the completion of the project, I used this commercial package. As this library was in C++, I coupled the library with the fluid solver based in Python. At every iteration of the time loop, the LHS matrix was passed to the library (C++) and a suitable preconditioner was computed using H-matrix algebra. This preconditioner was passed back to the Python solver and used to achieve an acceleration of 20%.